Summary of Structure

Array

Fixed Sized Sliding Window

Sliding Window Median 60%

Sliding Window Median
可以用two heap，也可以用multiset

Sliding Window Maximum
可以用deque
次优解是用heap + lazy deletion

Dynamic Sliding Window / Continuous Subarray

LC713 Subarray Product Less Than K

Input: nums = [10, 5, 2, 6], k = 100
Output: 8
Explanation: The 8 subarrays that have product less than 100 are: [10], [5], [2], [6], [10, 5], [5, 2], [2, 6], [5, 2, 6].
Note that [10, 5, 2] is not included as the product of 100 is not strictly less than k.

LC992 Subarrays with K Different Integers

Input: A = [1,2,1,2,3], K = 2
Output: 7
Explanation: Subarrays formed with exactly 2 different integers: [1,2], [2,1], [1,2], [2,3], [1,2,1], [2,1,2], [1,2,1,2].

LC340 Longest Substring with At Most K Distinct Characters

Input: s = "eceba", k = 2
Output: 3
Explanation: T is "ece" which its length is 3.

LC992和LC159思路类似，都是维护一个sliding window，然后用一个map保存table里面的内容（key -> element, value -> count）
992稍微复杂一些，需要维护两个sliding window，这两个window右边是对齐的，分别表示从左边到右边有K个数字的最大窗口和最小窗口

LC325 Maximum Size Subarray Sum Equals k

LC76 Minimum Window Substring

LC152. Maximum Product Subarray
是DP

LC828. Unique Letter String

Input: "ABC"
Output: 10
Explanation: All possible substrings are: "A","B","C","AB","BC" and "ABC".
Evey substring is composed with only unique letters.
Sum of lengths of all substring is 1 + 1 + 1 + 2 + 2 + 3 = 10

Input: "ABA"
Output: 8
Explanation: The same as example 1, except uni("ABA") = 1.

考虑按照subarray的起点分类

考虑按照每一个元素被几个subarray包含分类（左边界几种可能，右边界几种）
对于每一个字母，边界最远到达字符串结束或者下一个同类字符位置
比如 bdabbabbb，中间的a的左边界最多到第一个a，有3种，右边界到底，最多4种，一共有12个subarray包括了第二个a

Incontinuous Subarray

Find Next or Previous element in Array

Rain Water
Next equal or greater than
LC315 Count of Smaller Numbers After Self(??)

Split Array

Range / Overlap

google下雨
安排会议

Palindromic

LC5 Longest Palindromic Substring

Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.

回文有两种方法
DP P(i,j) = true 如果substring [i,j]是回文的
然后P(i,j) = (P(i+1,j-1) && Si == Sj)
base case: P(i, i) = true P(i, i+1) = Si == Si+1

还有从中间扩展
都是O(N^2)

Parenthesis

Permutation / Combination

LC552. Student Attendance Record II
DP即可

2-D Coordinate

可以按照对角线分，也可以投影到两个维度

LC939. Minimum Area Rectangle
直接遍历每一种对角点就行了

Matrix

LC240. Search a 2D Matrix II
直接可以排除一行或者一列

Tree

Binary Tree Inorder Traversal

在完全二叉树的最后一层做binary search：把传统的binary search的寻址方式改一下
数完全二叉树一共有几个节点：先确定深度，然后DFS确定最后一个元素的位置
给一个只有结构的二叉树和inorder array，重新填入值

序列化和反序列化

Segment Tree

Sliding Window Median 60%

Iterative Traversal

LC145 Binary Tree Postorder Traversal

summary
对于iterative traversal，一般方法是用一个stack，和一个指针
一个node有两次被访问的时候，第一次是指针指向它，然后压栈的时候，此时子树都没有访问，压栈之后指针指向左子树或者右子树
第二次是弹出的时候（当第一个访问的子树已经到底，开始弹出），此时压栈时候选择的子树已经访问完，指针应该指向另一个子树

对于preorder，在压栈的时候visit，然后指针指向左子树
弹出的时候指针指向右子树

对于inorder，压的时候不访问，然后指针指向左子树
弹出的时候visit，然后指针指向右子树

对于树的访问，不要像递归一样考虑单个子树（先左边完成，然后中间，然后右边）
而是考虑成单个点，这个点一定会被访问，而且是在左右子树都没有访问的时候（preorder）
在左子树访问完的时候（inorder）

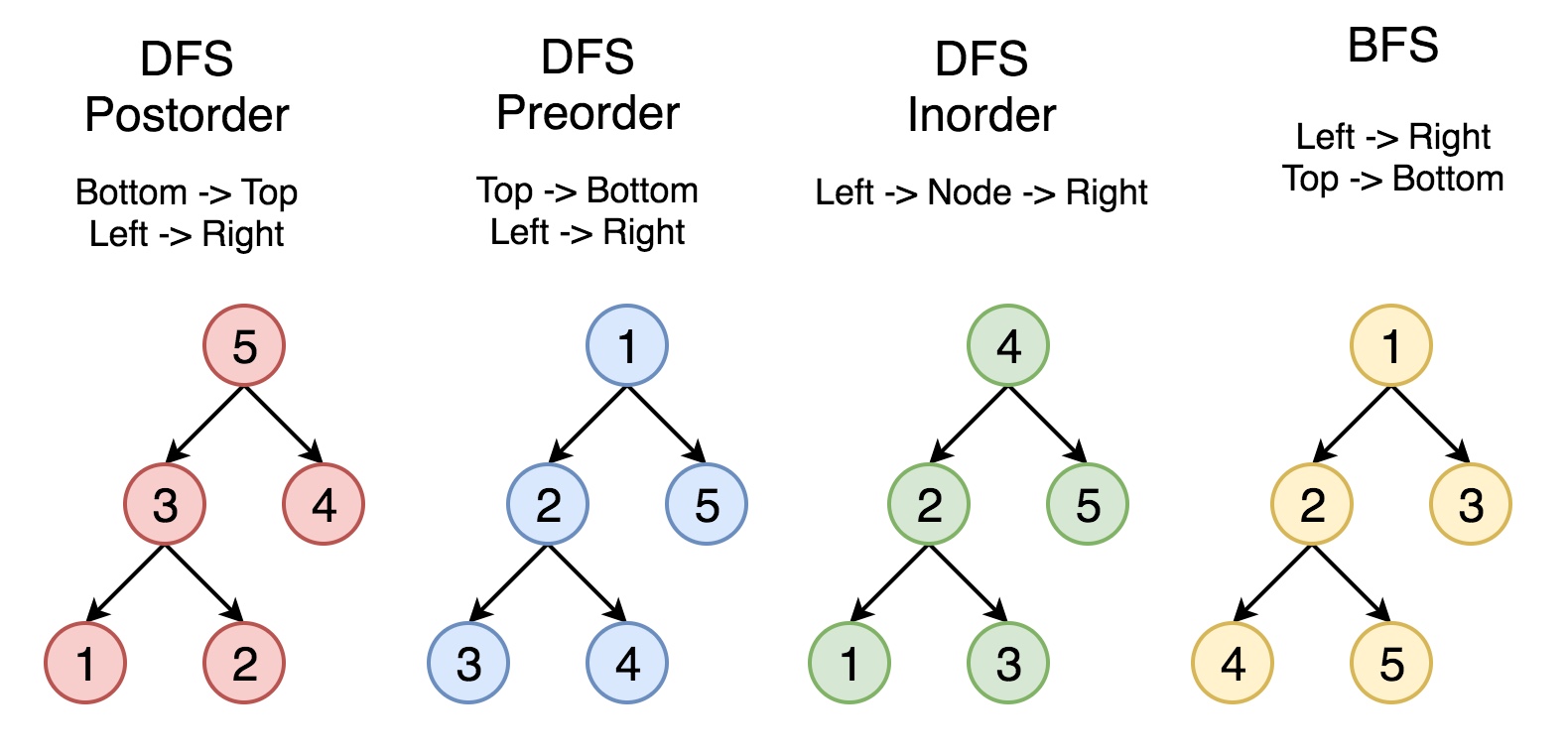
IMAGE

/* preorder/inorder traversal */
stack<int> s;
TreeNode *p = root;
while(!s.empty() || p!=nullptr) {
if(p!=nullptr) {
stack.push(p);
visit(p); // preorder的访问时间
p=p.left;
}
else {
p = stack.top();
stack.pop();
// inorder的访问时间
p = p.right;
}
}
/* preorder */
stack<int> s;
s.push(root);
while(!s.empty()) {
TreeNode *p = s.top();
s.pop();
visit(s);
if(p.left!=nullptr) {
s.push(p.left);
}
if(p.right!=nullptr) {
s.push(p.right);
}
}
/* inorder */
stack<int> s;
TreeNode *p = root;
while(!s.empty()||p!=nullptr) {
while(p!=nullptr) {
s.push(p);
p=p.left;
}
p=s.top();
s.pop();
visit(p);
p=p.right;
}

对于postorder，访问顺序等于preoder一个左右子树调换的树的反向
所以可以

/* postorder traversal */
stack<int> s;
TreeNode *p = root;
while(!s.empty() || p!=nullptr) {
if(p!=nullptr) {
stack.push(p);
visit_last(p); // preorder的访问时间
p=p.right;
}
else {
p = stack.top();
stack.pop();
p = p.left;
}
}

如果不用这个trick

/* postorder traversal*/
stack<pair<TreeNode*,bool>> s;
TreeNode *p = root;
vector<int> ans;
while(!s.empty() || p!=nullptr) {
if(p!=nullptr) {
s.push(make_pair(p,false));
p=p->left;
}
else {
p = s.top().first;
bool right_visited = s.top().second;
s.pop();
if(right_visited) {
ans.push_back(p->val);
p=nullptr;
}
else {
s.push(make_pair(p, true));
p = p->right;
}
}
}

Morris Traversal

/* Morris Traversal inorder */
1. Initialize current as root
2. While current is not NULL
If the current does not have left child
a) Print current’s data
b) Go to the right, i.e., current = current->right
Else
a) Make current as the right child of the rightmost
node in current's left subtree
b) Go to this left child, i.e., current = current->left
/* Morris preorder */
1...If left child is null, print the current node data. Move to right child.
….Else, Make the right child of the inorder predecessor point to the current node. Two cases arise:
………a) The right child of the inorder predecessor already points to the current node. Set right child to NULL. Move to right child of current node.
………b) The right child is NULL. Set it to current node. Print current node’s data and move to left child of current node.
2...Iterate until current node is not NULL.

Graph

Search (BFS/DFS)

LC1036 Escape a Large Maze

Normal BFS

LC490. The Maze

Input 1: a maze represented by a 2D array

0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0

Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (4, 4)

Output: true

Explanation: One possible way is : left -> down -> left -> down -> right -> down -> right.

BFS可以，但是DFS不行，因为在此题中，位置是唯一状态，与如何到达该位置无关
DFS+pruning（存position+direction）应该也可以

由此题开始，BFS和DFS的本质区别？
此题就是在一个有向图中搜索某一个点，由于和路径无关，只是找一个点，所以BFS比较合适
在图中DFS，任何一个时刻的状态是一条路径，而BFS，状态是一个波面和一个访问的点

DFS+pruning

LC490. The Maze
这题DFS+pruning可能也可以，但是normal BFS最方便

Dijkstra

LC505. The Maze II

Bidirectional BFS

Knight's Shortest Path on an Infinite Chessboard
LC127 Word Ladder
LC934 Shortest Bridge
LC433 Minimum Genetic Mutation

A-star search

LC773 Sliding Puzzle

Very Large Object

External Sort

TODO

LC145
LC773
LC315

Segment tree??

还没有归类的
sliding window maximum

Unclassified